化学反応式から、速度定数の単位を考える方法について例題付きで解説する。
速度定数とは
速度定数とは、化学反応において反応速度を求める際の比例定数。
反応A + 3B→ C + 2D の速度式は𝑣=𝑘[A][B]²であるとされたとき、この𝑘が速度定数に該当する。
【例題1】
(1)反応A + 3B→ C + 2D の速度式は𝑣=𝑘[A][B]²である。濃度がmol dm⁻³で表されるとき、𝑘の単位は何か。
★mol dm⁻³は、mol L⁻¹と等しいです。dm=10cmのことなので、dm³の量はは1Lということになります。
(2)この速度式を(i) A と(ii) C の消費と生成の速度によって表せ。
解答
(1)
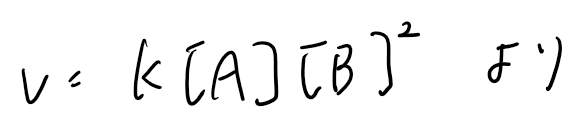
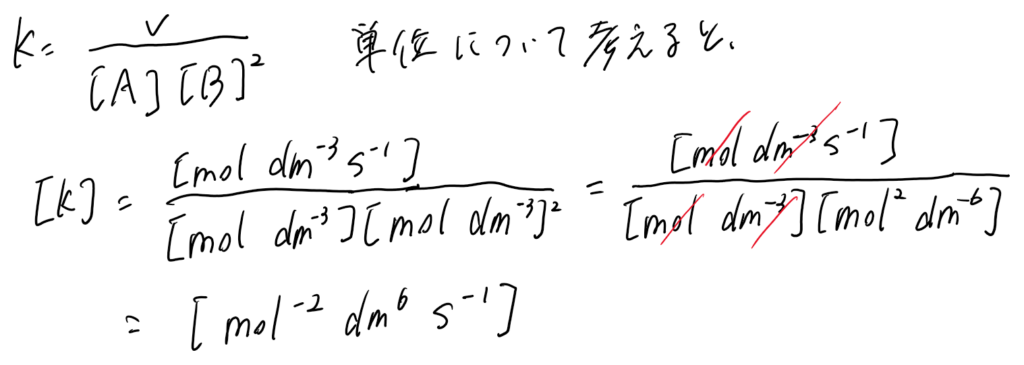
𝑘の単位は mol⁻²dm⁶s⁻¹ となる。
(2)
(i) A は矢印の左側の文字なので消費されている。
$$\frac{-d[A]}{dt}=𝑣$$
ちなみにBも同様で$$\frac{-d[B]}{dt}=3𝑣$$
係数のつけ方についてはこちらをチェック!
(ii)Cは矢印の右側の文字なので生成されている。
$$\frac{d[C]}{dt}=𝑣$$
ちなみにDも同様で$$\frac{d[D]}{dt}=2𝑣$$
【例題2】
速度式が,(i) mol dm⁻³で表した濃度,(ii) kPaで表した圧力,で表されるとする。2次と3次の速度定数の単位は何か
解答
速度式を2次のときは𝑣=𝑘[A]²、3次のときは𝑣=𝑘[A]³ と表すことができる。
(i)
[𝑣]= mol dm⁻³ s⁻¹、[A]= mol dm⁻³のとき、
2次のとき、[𝑘]=[mol dm⁻³ s⁻¹][mol dm⁻³]⁻²=mol⁻¹dm³s⁻¹
3次のとき、[𝑘]=[mol dm⁻³ s⁻¹][mol dm⁻³]⁻³=mol⁻²dm⁶s⁻¹
(ii)
[𝑣]= kPa s⁻¹、[A]= kPa のとき、
2次のとき、[𝑘]=[kPa s⁻¹][kPa]⁻²=kPa⁻¹s⁻¹
3次のとき、[𝑘]=[kPa s⁻¹][kPa]⁻³=kPa⁻²s⁻¹
まとめ
単位を考える問題(例えば物理などの単位換算で両辺の単位が一致するか確認するとき)と同様に考えて解けばよい。



